On souhaite réaliser le logo représenté par la surface colorée de la figure ci-contre.

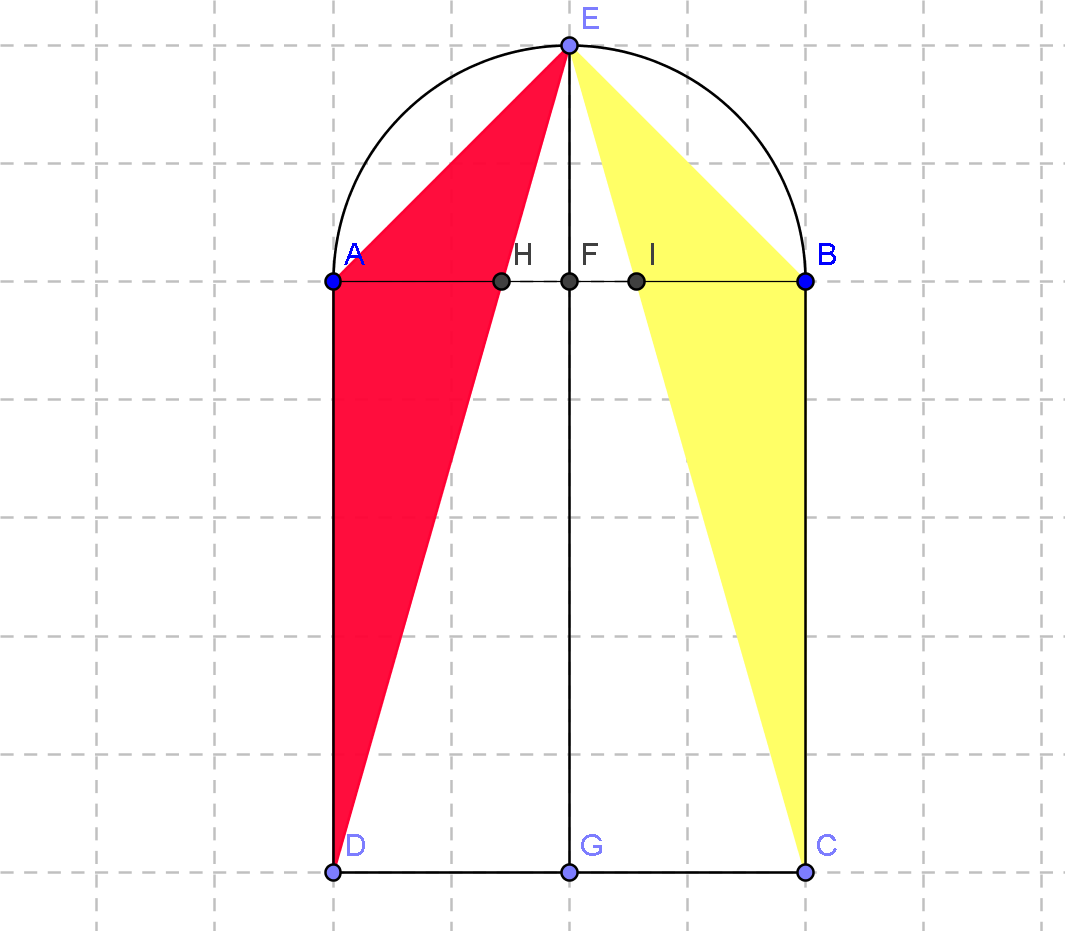
On considère un rectangle ABCD, le demi-cercle de diamètre [AB] situé à l'extérieur du rectangle et le point E du demi-cercle tel que EA = EB.

Les dimensions sont AB = 40 cm et AD = 60 cm.

F et G sont les projections orthogonales de E sur [AB] et [CD]. [ED] coupe [AB] en H et [EC] coupe [AB] en I .